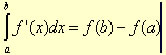Project Snyder-Calculus

Home
Professional
Classes
Personal
- Local
- West Branch
- Arkansas
- Backpacking
- Family

AP Calculus Syllabus

College Board

AP® CALCULUS AB
SYLLABUS

COURSE OVERVIEW

AP Calculus is one of the most rigorous and challenging mathematics classes that is offered at our high school. The course is for students that have completed coursework in Algebra I, Algebra II, Geometry and Pre-Calculus with Trigonometry. The course emphasize that students work with functions graphically, numerically, analytically and verbally. The course gives emphasis to the connections between these representations.

COURSE RESOURCES
Primary textbook:
Calculus: Concepts and Applications
Key Curriculum Press, ©2005, ISBN 1-55953-654-3,
Paul A. Foerster

Supplemental Resources:
Calculus: Concepts and Applications Instructor’s Resource Book
Key Curriculum Press, ©2005, ISBN 1-55953-656-X
Paul A. Foerster

Multiple-Choice & Free-Response Questions in Preparation for the AP Calculus (AB) Examination (8th Edition)
D & S Marketing Systems, Inc., ©2003
David Lederman and Lin McMullin
.
STUDENT EVALUATION
Students will evaluated on tests and quiz scores, oral presentations, written reports, assignments, past AP Exams, use of Geometer’s Sketch Pad for explorations of concepts, open-ended questions requiring written explanation and working in collaborative groups. Throughout the course students will be indirectly evaluated on the use of a graphing calculator. For example, students will have to integrate and differentiate functions numerically using a graphing calculator. Students will also use a graphing calculator to examine extrema and behavior of functions, find limits and determine differentiability and continuity.

COURSE OUTLINE

CHAPTER 1 (10 days)
Limits, Derivatives, Integrals, and Integrals
1-1 The Concept of Instantaneous Rate
1-2 Rate of Change by Equation, Graph, or Table
1-3 One Type of Integral of a Function
1-4 Definite Integrals by Trapezoids, from Equations and Data

CHAPTER 2 (16 days)
Properties of Limits
2-1 Numerical Approach to the Definition of Limit
2-2 Graphical and Algebraic Approaches to the Definition of Limit
2-3 The Limit Theorems
2-4 Continuity and Discontinuity
2-5 Limits Involving Infinity
2-6 The Intermediate Value Theorem and Its Consequences

CHAPTER 3 (18 days)
Derivatives, Antiderivatives, and Indefinite Integrals
3-1 Graphical Interpretation of Derivative
3-2 Difference Quotients and One Definition of Derivative
3-3 Derivative Functions, Numerically and Graphically
3-4 Derivative of the Power Function and Another Definition of Derivative
3-5 Displacement, Velocity, and Acceleration
3-6 Introduction to Sine, Cosine, and Composite Functions
3-7 Derivatives of Composite Functions—The Chain Rule
3-8 Proof and Application of Sine and Cosine Derivatives
3-9 Exponential and Logarithmic Functions

CHAPTER 4 (25 days)
Products, Quotients, and Parametric Functions
4-1 Combinations of Two Functions
4-2 Derivative of a Product of Two Functions
4-3 Derivative of a Quotient of Two Functions
4-4 Derivatives of the Other Trigonometric Functions
4-5 Derivatives of Inverse Trigonometric Functions
4-6 Differentiability and Continuity
4-7 Derivatives of a Parametric Function
4-8 Graphs and Derivatives of Implicit Relations
4-9 Related Rates

CHAPTER 5 (25 days)
Definite and Indefinite Integrals
5-1 A Definite Integral Problem
5-2 Linear Approximations and Differentials
5-3 Formal Definition of Antiderivative and Indefinite Integral
5-4 Riemann Sums and the Definition of Definite Integral
5-5 The Mean Value Theorem and Rolle’s Theorem
5-6 The Fundamental Theorem of Calculus
5-7 Definite Integral Properties and Practice
5-8 Definite Integrals Applied to Area and Other Problems
5-9 Volume of a Solid by Plane Slicing
5-10 Definite Integrals Numerically by Grapher and by Simpson’s Rule

CHAPTER 6 (15 days)
The Calculus of Exponential and Logarithmic Functions
6-1 Integral of the Reciprocal Function: A Population Growth Problem
6-2 Antiderivative of the Reciprocal Function and Another Form of the Fundamental Theorem
6-4 The Number e, Exponential Functions, and Logarithmic Differentiation
6-5 Limits of Indeterminate Forms: l’Hospital’s Rule
6-6 Derivative and Integral Practice for Transcendental Functions

CHAPTER 7 (14 days)
The Calculus of Growth and Decay
7-1 Direct Proportion Property of Exponential Functions
7-2 Exponential Growth and Decay
7-4 Graphical Solution of Differential Equations by Using Slope Fields
7-5 Numerical Solution of Differential Equations by Using Euler’s Method

CHAPTER 8 (14 days)
The Calculus of Plane and Solid Figures
8-2 Critical Points and Points of Inflection
8-3 Maxima and Minima in Plane and Solid Figures

CHAPTER 10 (14 days)
The Calculus of Motion—Averages, Extremes
10-1 Introduction to Distance and Displacement for Motion Along a Line
10-2 Distance, Displacement, and Acceleration for Linear Motion
10-3 Average Value Problems in Motion and Elsewhere
10-4 Minimal Path Problems
10-5 Maximum and Minimum Problems in Motion and Elsewhere

AFTER THE AP EXAM
CHAPTER 8
The Calculus of Plane and Solid Figures
8-4 Volume of a Solid of Revolution by Cylindrical Shells
8-5 Length of a Plane Curve—Arc Length

CHAPTER 9
Algebraic Calculus Techniques for the Elementary Functions
9-1 Introduction to the Integral of a Product of Two Functions
9-2 Integration by Parts—A Way to Integrate Products
9-3 Rapid Repeated Integration by Parts

CORRELATIONS TO AP COURSE DESCRIPTION

I. Functions, Graphs, and Limits

1. Analysis of graphs

Throughout

2. Limits of functions (including one-sided limits)

An intuitive understanding of the limiting process
Calculating limits using algebra
Estimating limits from graphs or tables of data

Chapters 1 and 2

Sections 2-1, 2-2, 2-3, and 2-5

Chapter 1 and Section 2-2

3. Asymptotic and unbounded behavior

Understanding asymptotes in terms of graphical behavior
Describing asymptotic behavior in terms of limits involving infinity
Comparing relative magnitudes of functions and their rates of change (e.g., contrasting exponential growth, polynomial growth, and logarithmic growth)

Section 2-5

Chapters 3 and 6

4. Continuity as a property of functions

An intuitive understanding of continuity (Close values of the domain lead to close values of the range)
Understanding continuity in terms of limits
Geometric understanding of graphs of continuous functions (intermediate value theorem and extreme value theorem)

Section 2-4

II. Derivatives

1. Concept of the derivative

Derivative presented graphically, numerically, and analytically
Derivative interpreted as an instantaneous rate of change
Derivative defined as the limit of the difference quotient
Relationship between differentiability and continuity

Sections 3-1, 3-2, 3-3, and 3-4

Sections 1-2, 3-5, and throughout
Sections 3-2 and 3-4

Section 4-6

2. Derivative at a point

Slope of a curve at a point. Examples are emphasized, including points at which there are vertical tangents and points at which there are no tangents.
Tangent line to a curve at a point and local linear approximation
Instantaneous rate of change as the limit of average rate of change
Approximate rate of change from graphs and tables of values

Sections 3-1 and 8-2

Section 3-2

Section 1-2, 3-2, and 3-4

Sections 1-2 and 3-3

3. Derivative as a function

Corresponding characteristics of graphs of f and f′
Relationship between the increasing and decreasing behavior of f and the sign of f′
The mean value theorem and its geometric consequences
Equations involving derivatives. Verbal descriptions are translated into equations involving derivatives and vice versa.

Sections 3-3 and 8-2

Section 5-5

Sections 7-2 and 7-3

4. Second derivatives

Corresponding characteristics of the graphs of f, f’ and f’’
Relationship between the concavity of f and the sign of f’’
Points of inflection as places where concavity changes

Section 8-2

5. Applications of derivatives

Analysis of curves, including the notion of monotonicity and concavity
Optimization, both absolute (global) and relative (local) extrema
Modeling rates of change, including related rates problems
Use of implicit differentiation to find the derivative of an inverse function
Interpretation of the derivative as a rate of change in varied applied contexts, including velocity, speed, and acceleration
Geometric interpretation of differential equations via slope fields and the relationship between slope fields and solution curves for differential equations

Section 8-2

Sections 8-2, 8-3, and 10-5

Section 4-9

Sections 3-9 and 4-5

Sections 1-2, 3-5, and 4-9

Sections 7-4 and 7-6

6. Computation of derivatives

Knowledge of derivatives of basic functions, including power, exponential, logarithmic, trigonometric, and inverse trigonometric functions.
Basic rules for the derivatives of sums, products, and quotients of functions
Chain rule and implicit differentiation

Sections 3-4, 3-8, 3-9, 4-4, and 4-5

Sections 4-1, 4-2, and 4-3

Sections 3-7 and 4-8

II. Integrals

1. Interpretation and properties of definite integrals

Computation of Riemann sums using left, right, and midpoint evaluation points
Definite integral as a limit of the rate of change of a quantity over an interval interpreted as the change of the quantity over the interval:
Basic properties of definite integrals (e.g., additivity and linearity)

Section 5-4

Sections 5-4 and 5-6

Sections 5-3 and 5-7

2. Applications of integrals (includes finding the area of a region, the volume of a solid with known cross sections, the average value of a function, and the distance traveled by a particle along a line)

Sections 5-8, 5-9, 10-1, 10-2, and 10-3

3. Fundamental theorem of calculus

Use of the fundamental theorem to evaluate definite integrals
Use of the fundamental theorem to represent a particular antiderivative, and the analytical and graphical analysis of functions so defined

Sections 5-6 and 5-7

4. Techniques of antidifferentiation

• Antiderivatives following directly from derivatives of basic functions
Antiderivatives by substitution of variables (including change of limits for definite integrals)

Section 5-3

5. Applications of antidifferentiation

Finding specific antiderivatives using initial conditions, including applications to motion along a line
Solving separable differential equations and using them in modeling (in particular, studying the equation y′ = ky and exponential growth)

Sections 5-3, 5-8, 10-1, and 10-2

Sections 7-2 and 7-3

6. Numerical approximations to definite integrals.

Use of Riemann sums and trapezoidal sums to approximate definite integrals of functions represented algebraically, graphically, and by tables of values.

Sections 1-3, 1-4, and 5-4